Pengertian dan Analisis Korelasi Sederhana dengan Rumus Pearson
Pengertian dan Analisis Korelasi Sederhana dengan Rumus Pearson
– Korelasi Sederhana merupakan suatu Teknik Statistik yang dipergunakan
untuk mengukur kekuatan hubungan 2 Variabel dan juga untuk dapat
mengetahui bentuk hubungan antara 2 Variabel tersebut dengan hasil yang
sifatnya kuantitatif. Kekuatan hubungan antara 2 variabel yang dimaksud
disini adalah apakah hubungan tersebut ERAT, LEMAH, ataupun TIDAK ERAT
sedangkan bentuk hubungannya adalah apakah bentuk korelasinya Linear
Positif ataupun Linear Negatif.
Disamping Korelasi, Diagram Tebar (Scatter Diagram) sebenarnya juga
dapat mempelajari hubungan 2 variabel dengan cara menggambarkan hubungan
tersebut dalam bentuk grafik. Tetapi Diagram tebar hanya dapat
memperkirakan kecenderungan hubungan tersebut apakah Linear Positif,
Linear Negatif ataupun tidak memiliki Korelasi Linear. Kelemahan Diagram
Tebar adalah tidak dapat menunjukkan secara tepat dan juga tidak dapat
memberikan angka Kuantitas tentang kekuatan hubungan antara 2 variabel
yang dikaji tersebut.
Kekuatan Hubungan antara 2 Variabel biasanya disebut dengan Koefisien
Korelasi dan dilambangkan dengan symbol “r”. Nilai Koefisian r akan
selalu berada di antara -1 sampai +1.
Perlu diingat :
Koefisien Korelasi akan selalu berada di dalam Range -1 ≤ r ≤ +1
Jika ditemukan perhitungan diluar Range tersebut, berarti telah terjadi kesalahan perhitungan dan harus di koreksi terhadap perhitungan tersebut.
Rumus yang dipergunakan untuk menghitung Koefisien Korelasi Sederhana adalah sebagai berikut :
(Rumus ini disebut juga dengan Pearson Product Moment)
r = nΣxy – (Σx) (Σy)
. √{nΣx² – (Σx)²} {nΣy2 – (Σy)2}
Dimana :
n = Banyaknya Pasangan data X dan Y
Σx = Total Jumlah dari Variabel X
Σy = Total Jumlah dari Variabel Y
Σx2= Kuadrat dari Total Jumlah Variabel X
Σy2= Kuadrat dari Total Jumlah Variabel Y
Σxy= Hasil Perkalian dari Total Jumlah Variabel X dan Variabel Y
Apabila Nilai Koefisien Korelasi mendekati +1 (positif Satu) berarti pasangan data Variabel X dan Variabel Y memiliki Korelasi Linear Positif yang kuat/Erat.
Apabila Nilai Koefisien Korelasi mendekati -1 (Negatif Satu) maka hal ini menunjukan pasangan data Variabel X dan Variabel Y memiliki Korelasi Linear Negatif yang kuat/erat.
Apabila Nilai Koefisien Korelasi mendekati 0 (Nol) berarti pasangan data Variabel X dan Variabel Y memiliki korelasi yang sangat lemah atau berkemungkinan tidak berkorelasi.
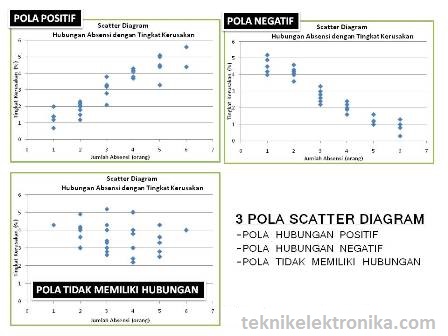
Ketiga Pola atau bentuk hubungan tersebut jika di gambarkan ke dalam Scatter Diagram (Diagram tebar) adalah sebagai berikut :
Kemudian hitunglah Koefisien Korelasi berdasarkan rumus korelasi dibawah ini :
r = nΣxy – (Σx) (Σy)
. √{nΣx² – (Σx)²} {nΣy2 – (Σy)2}
r = (30 . 6861) – (699) (282)
. √{30. 16487 – (699)²} {30 . 3112 – (282)2}
r = (205830) – (197118)
. √{494610 – 488601} {93360 – 75924}
r = 8712
. 9118.13
r = 0.955
Jadi Koefisien Korelasi antara Suhu Ruangan dan Jumlah Cacat Produksi adalah 0.955, berarti kedua variabel tersebut memiliki hubungan yang ERAT dan bentuk hubungannya adalah Linear Positif.
Jika Hubungan Suhu Ruangan dan Jumlah Cacat Produksi dibuat dalam bentuk Scatter Diagram (Diagram Tebar), maka bentuknya akan seperti dibawah ini :
Analisis Korelasi (Correlation Analysis) juga merupakan salah satu alat (tool) yang digunakan dalam Metodologi Six Sigma di Tahap Analisis.
Untuk mempermudah kita dalam Menghitung Koefisien Korelasi, kita juga dapat menggunakan Microsoft Excel.
Perlu diingat :
Koefisien Korelasi akan selalu berada di dalam Range -1 ≤ r ≤ +1
Jika ditemukan perhitungan diluar Range tersebut, berarti telah terjadi kesalahan perhitungan dan harus di koreksi terhadap perhitungan tersebut.
Rumus Pearson Product Moment
Koefisien Korelasi Sederhana disebut juga dengan Koefisien Korelasi Pearson karena rumus perhitungan Koefisien korelasi sederhana ini dikemukakan oleh Karl Pearson yaitu seorang ahli Matematika yang berasal dari Inggris.Rumus yang dipergunakan untuk menghitung Koefisien Korelasi Sederhana adalah sebagai berikut :
(Rumus ini disebut juga dengan Pearson Product Moment)
r = nΣxy – (Σx) (Σy)
. √{nΣx² – (Σx)²} {nΣy2 – (Σy)2}
Dimana :
n = Banyaknya Pasangan data X dan Y
Σx = Total Jumlah dari Variabel X
Σy = Total Jumlah dari Variabel Y
Σx2= Kuadrat dari Total Jumlah Variabel X
Σy2= Kuadrat dari Total Jumlah Variabel Y
Σxy= Hasil Perkalian dari Total Jumlah Variabel X dan Variabel Y
Pola / Bentuk Hubungan antara 2 Variabel :
1. Korelasi Linear Positif (+1)
Perubahan salah satu Nilai Variabel diikuti perubahan Nilai Variabel yang lainnya secara teratur dengan arah yang sama. Jika Nilai Variabel X mengalami kenaikan, maka Variabel Y akan ikut naik. Jika Nilai Variabel X mengalami penurunan, maka Variabel Y akan ikut turun.Apabila Nilai Koefisien Korelasi mendekati +1 (positif Satu) berarti pasangan data Variabel X dan Variabel Y memiliki Korelasi Linear Positif yang kuat/Erat.
2. Korelasi Linear Negatif (-1)
Perubahan salah satu Nilai Variabel diikuti perubahan Nilai Variabel yang lainnya secara teratur dengan arah yang berlawanan. Jika Nilai Variabel X mengalami kenaikan, maka Variabel Y akan turun. Jika Nilai Variabel X mengalami penurunan, maka Nilai Variabel Y akan naik.Apabila Nilai Koefisien Korelasi mendekati -1 (Negatif Satu) maka hal ini menunjukan pasangan data Variabel X dan Variabel Y memiliki Korelasi Linear Negatif yang kuat/erat.
3. Tidak Berkorelasi (0)
Kenaikan Nilai Variabel yang satunya kadang-kadang diikut dengan penurunan Variabel lainnya atau kadang-kadang diikuti dengan kenaikan Variable yang lainnya. Arah hubungannya tidak teratur, kadang-kadang searah, kadang-kadang berlawanan.Apabila Nilai Koefisien Korelasi mendekati 0 (Nol) berarti pasangan data Variabel X dan Variabel Y memiliki korelasi yang sangat lemah atau berkemungkinan tidak berkorelasi.
Ketiga Pola atau bentuk hubungan tersebut jika di gambarkan ke dalam Scatter Diagram (Diagram tebar) adalah sebagai berikut :

Tabel tentang Pedoman umum dalam menentukan Kriteria Korelasi :
| r | Kriteria Hubungan |
| 0 | Tidak ada Korelasi |
| 0 – 0.5 | Korelasi Lemah |
| 0.5 – 0.8 | Korelasi sedang |
| 0.8 – 1 | Korelasi Kuat / erat |
| 1 | Korelasi Sempurna |
Contoh Penggunaan Analisis Korelasi di Produksi :
- Apakah ada hubungan antara suhu ruangan dengan jumlah cacat Produksi?
- Apakah ada hubungan antara lamanya waktu kerusakan mesin dengan jumlah cacat produksi?
- Apakah ada hubungan antara jumlah Jam lembur dengan tingkat absensi?
Contoh Kasus Analisis Korelasi Sederhana :
Seorang Engineer ingin mempelajari apakah adanya pengaruh Suhu Ruangan terhadap Jumlah Cacat yang dihasilkan dan juga ingin mengetahui keeratan serta bentuk hubungan antara dua variabel tersebut. Engineer tersebut kemudian mengambil data selama 30 hari terhadap rata-rata (mean) suhu ruangan dan Jumlah Cacat Produksi seperti dibawah ini :| Tanggal | Rata-rata Suhu Ruangan | Jumlah Cacat |
| 1 | 24 | 10 |
| 2 | 22 | 5 |
| 3 | 21 | 6 |
| 4 | 20 | 3 |
| 5 | 22 | 6 |
| 6 | 19 | 4 |
| 7 | 20 | 5 |
| 8 | 23 | 9 |
| 9 | 24 | 11 |
| 10 | 25 | 13 |
| 11 | 21 | 7 |
| 12 | 20 | 4 |
| 13 | 20 | 6 |
| 14 | 19 | 3 |
| 15 | 25 | 12 |
| 16 | 27 | 13 |
| 17 | 28 | 16 |
| 18 | 25 | 12 |
| 19 | 26 | 14 |
| 20 | 24 | 12 |
| 21 | 27 | 16 |
| 22 | 23 | 9 |
| 23 | 24 | 13 |
| 24 | 23 | 11 |
| 25 | 22 | 7 |
| 26 | 21 | 5 |
| 27 | 26 | 12 |
| 28 | 25 | 11 |
| 29 | 26 | 13 |
| 30 | 27 | 14 |
Penyelesaian :
Pertama-tama hitunglah X², Y², XY dan totalnya seperti tabel dibawah ini :| Tanggal | Rata-rata Suhu Ruangan (X) | Jumlah Cacat (Y) | X2 | Y2 | XY |
| 1 | 24 | 10 | 576 | 100 | 240 |
| 2 | 22 | 5 | 484 | 25 | 110 |
| 3 | 21 | 6 | 441 | 36 | 126 |
| 4 | 20 | 3 | 400 | 9 | 60 |
| 5 | 22 | 6 | 484 | 36 | 132 |
| 6 | 19 | 4 | 361 | 16 | 76 |
| 7 | 20 | 5 | 400 | 25 | 100 |
| 8 | 23 | 9 | 529 | 81 | 207 |
| 9 | 24 | 11 | 576 | 121 | 264 |
| 10 | 25 | 13 | 625 | 169 | 325 |
| 11 | 21 | 7 | 441 | 49 | 147 |
| 12 | 20 | 4 | 400 | 16 | 80 |
| 13 | 20 | 6 | 400 | 36 | 120 |
| 14 | 19 | 3 | 361 | 9 | 57 |
| 15 | 25 | 12 | 625 | 144 | 300 |
| 16 | 27 | 13 | 729 | 169 | 351 |
| 17 | 28 | 16 | 784 | 256 | 448 |
| 18 | 25 | 12 | 625 | 144 | 300 |
| 19 | 26 | 14 | 676 | 196 | 364 |
| 20 | 24 | 12 | 576 | 144 | 288 |
| 21 | 27 | 16 | 729 | 256 | 432 |
| 22 | 23 | 9 | 529 | 81 | 207 |
| 23 | 24 | 13 | 576 | 169 | 312 |
| 24 | 23 | 11 | 529 | 121 | 253 |
| 25 | 22 | 7 | 484 | 49 | 154 |
| 26 | 21 | 5 | 441 | 25 | 105 |
| 27 | 26 | 12 | 676 | 144 | 312 |
| 28 | 25 | 11 | 625 | 121 | 275 |
| 29 | 26 | 13 | 676 | 169 | 338 |
| 30 | 27 | 14 | 729 | 196 | 378 |
| Total | 699 | 282 | 16487 | 3112 | 6861 |
r = nΣxy – (Σx) (Σy)
. √{nΣx² – (Σx)²} {nΣy2 – (Σy)2}
r = (30 . 6861) – (699) (282)
. √{30. 16487 – (699)²} {30 . 3112 – (282)2}
r = (205830) – (197118)
. √{494610 – 488601} {93360 – 75924}
r = 8712
. 9118.13
r = 0.955
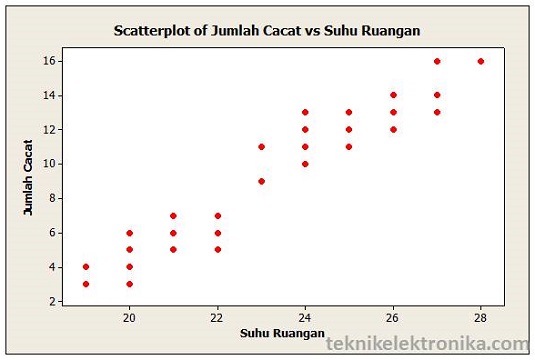
Jadi Koefisien Korelasi antara Suhu Ruangan dan Jumlah Cacat Produksi adalah 0.955, berarti kedua variabel tersebut memiliki hubungan yang ERAT dan bentuk hubungannya adalah Linear Positif.
Jika Hubungan Suhu Ruangan dan Jumlah Cacat Produksi dibuat dalam bentuk Scatter Diagram (Diagram Tebar), maka bentuknya akan seperti dibawah ini :

Analisis Korelasi (Correlation Analysis) juga merupakan salah satu alat (tool) yang digunakan dalam Metodologi Six Sigma di Tahap Analisis.
Untuk mempermudah kita dalam Menghitung Koefisien Korelasi, kita juga dapat menggunakan Microsoft Excel.
Tidak ada komentar:
Posting Komentar